Introdução
ao MATLAB
e
ao pacote GAAL
1.
Soma de Vetores e Multiplicação
por um escalar
1. Soma de Vetores e
Multiplicação por um escalar
Vetor é um conjunto de variáveis homogêneas (conteúdo do mesmo tipo) identificadas por um nome e individualizadas por meio de índices. No MATLAB, um vetor pode ser definido elemento por elemento, separados por brancos ou vírgulas. Para criarmos um vetor com 3 elementos fazemos:
EDU» b=[2 4 6]; ou EDU» b=[2,4,6];
1.1 Operações Elementares com Vetores
Abaixo há um quadro onde listamos as principais operações
feitas com vetores:
Operação |
Descrição
|
V+W |
Efetua a soma de dois vetores |
V-W |
Efetua a subtração de dois vetores |
Num*V |
Produto escalar de
num pelo vetor V |
Exemplo 1: Consideremos os vetores V=[1 2 3] e W=[1 4 2]. Vamos realizar as operações listadas na tabela acima sobre estes vetores.
EDU» V=[1 2 3];
% declaração do vetor V
EDU» W=[1 4 2]; %
declaração do vetor W
EDU» V+W
% soma dos vetores V e W
ans =
2 6
5
EDU» V-W
% subtração dos vetores V e W
ans =
0 -2 1
EDU» 2*V
% multiplicação do vetor V pelo escalar 2.
ans =
2 4
6
EDU» 5*W
% multiplicação do vetor V pelo escalar 5.
ans =
5 20
10
Na criação de um vetor, se os incrementos entre os elementos forem iguais, podemos utilizar a seguinte expressão:
c= <valor inicial> : <incremento> : <valor final>
Assim, para criarmos um vetor com o primeiro elemento igual a 10, o segundo igual a 15, o terceiro igual a 20 e assim sucessivamente até o último igual a 40 basta definir:
EDU» c=10:5:40
c =
10 15
20 25 30
35 40
Se o incremento desejado for igual a 1, então ele poderá ser omitido
EDU» v=3:7
v =
3 4
5 6 7
Ao invés de usar um incremento, um vetor pode também ser construído definindo o número desejado de elementos usando a função linspace, cuja sintaxe é:
linspace(<valor_inicial> , <valor_final>, <número_de_elementos)
Assim, para criarmos um vetor com primeiro elemento 10, último elemento 40 e com 7 elementos, fazemos:
EDU» a=linspace(10,40,7)
a =
10 15 20 25 30 35 40
Isto produz um vetor idêntico a c=10:5:40 definido acima. Se no comando linspace o parâmetro <número_de_elementos> for omitido serão gerados 100 pontos.
Os elementos de um vetor também podem ser referenciados individualmente:
EDU» c(2) %
segundo elemento de c
ans =
15
ou em blocos,
EDU» c(3:5) %
terceiro ao quinto elemento de c
ans =
20 25
30
Nos exemplos acima, os vetores possuem uma linha e várias colunas, sendo também chamados de vetores linha. Do mesmo modo podem existir vetores coluna, ou seja, vetores que possuem várias linhas e uma única coluna. Para criarmos um vetor coluna elemento por elemento, estes devem estar separados por (;). Vamos criar um vetor coluna com os seguintes elementos: 1 3 5.
EDU» v=[1; 3; 5;]
% gera um vetor coluna
v =
1
3
5
Para transformar um vetor linha em um vetor
coluna e vice-versa, usamos o operador de transposição (‘):
EDU» w=v' % obtém
o vetor linha a partir de um vetor coluna
w =
1 3
5
EDU» x=(1:2:5)' %
obtém o vetor coluna a partir de um vetor linha
x =
1
3
5
Para saber o comprimento de um vetor, ou seja, o número de elementos de um vetor, usamos o comando length. Assim, para determinar o tamanho do vetor x declarado acima, basta executar o comando:
EDU» length(x)
ans =
3
1.2 Comandos
gráficos do pacote GAAL
O pacote GAAL oferece alguns comandos para visualizar algumas das principais operações feitas com vetores. Alguns desses comandos estão contidos no quadro abaixo:
Operação |
Descrição
|
desvet(P) |
Desenha o vetor V com origem no ponto O=(0,0,0). |
desvet(P,V) |
Desenha o vetor V com origem no ponto P. |
axiss |
Reescala o eixo com a mesma escala. |
eixos |
Desenha os eixos
coordenados. |
box |
Desenha ou retira
uma caixa em volta da figura. |
rota |
Faz uma rotação em
torno do eixo z. |
ilsvw(V,W)
|
Visualiza a soma de
dois vetores. |
ilav(a,V) |
Visualiza a
multiplicação do vetor V pelo escalar a. |
Exemplo 2: Vamos
demonstrar alguns destes comandos através deste exemplo.
EDU» v=[1 2 3]; % cria o vetor v
EDU» w=[3 7 2]; % cria o vetor w
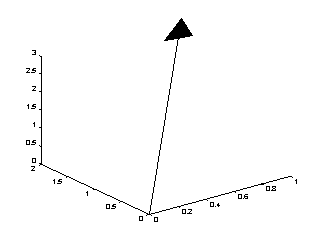
EDU» desvet(v) % desenha o vetor v
A
execução deste comando produz o seguinte resultado:
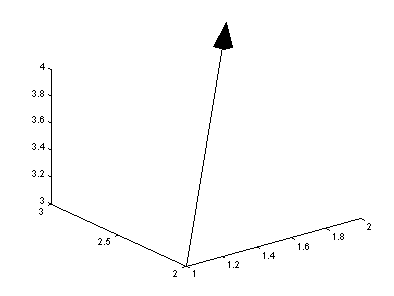
EDU»
desvet(v,[1,1,1]) % desenha o vetor
v com origem no ponto (1,1,1).
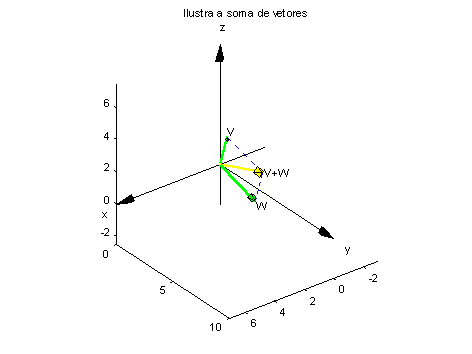
EDU» ilsvw(v,w)
% desenha a soma dos vetores v e w
EDU» grid off % retira as grades do desenho
EDU» box % retira a caixa que está em volta da figura
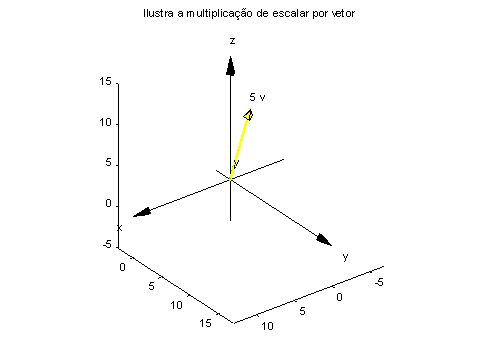
EDU» ilav(5,v)
% multiplica o vetor v pelo escalar 5.
EDU» grid off % retira as grades do desenho
EDU» box
% retira a caixa que está em volta da figura
O
comando rota faz com que vejamos com
mais clareza o resultado de cada
comando gráfico citado acima.
2. Produto de Vetores
Nesta seção, vamos utilizar os comandos do pacote GAAL para obter e visualizar o produto vetorial e escalar de vetores.
|
Função |
Descrição |
|
pe(V,W) |
Calcula o produto escalar do vetor V pelo vetor W |
|
pv(V,W) |
Calcula o produto vetorial do vetor V pelo vetor W |
|
no(V) |
Calcula a norma do vetor V |
|
V=randi(1,3) |
Cria um vetor aleatório com componentes inteiras |
Exemplo 3: Consideremos
dois vetores V e W gerados aleatoriamente. Vamos realizar as operações listadas
na tabela acima sobre estes vetores.
EDU» V=randi(1,3) % gera um vetor aleatório de três
elementos.
V =
5 -3 1
EDU» W=randi(1,3) % gera um vetor aleatório de três
elementos.
W =
0 4 3
EDU» pe(V,W) % produto escalar do vetor V pelo vetor W.
ans =
-9
EDU» pv(V,W) % produto vetorial do vetor V pelo vetor W.
ans =
-13 -15 20
EDU» no(V) % norma do vetor V.
ans =
35^(1/2) % ![]()
EDU» no(W) % norma do vetor W.
ans =
5
2.1 Comandos
gráficos do pacote GAAL
O pacote GAAL oferece alguns comandos para visualizar
o produto de dois vetores e a projeção de um vetor em outro. Alguns desses
comandos estão contidos no quadro abaixo:
Operação |
Descrição
|
ilvijk(V) |
Desenha o vetor V como soma de múltiplos escalares (combinação linear) dos vetores i,j,k. |
ilvxw(V,W)
|
Visualiza o produto vetorial VxW. |
ilproj(W,V)
|
Visualiza a projeção de V em W. |
eixos |
Desenha os eixos
coordenados. |
box |
Desenha ou retira
uma caixa em volta da figura. |
rota |
Faz uma rotação em
torno do eixo z. |
Exemplo 4: Vamos demonstrar alguns destes comandos neste
exemplo:
EDU» v=[2 4 6]; % cria o vetor v
EDU» w=[3 1 5]; % cria o vetor w
EDU» ilvijk(v) % desenha o vetor v como combinação linear dos vetores
i,j,k.
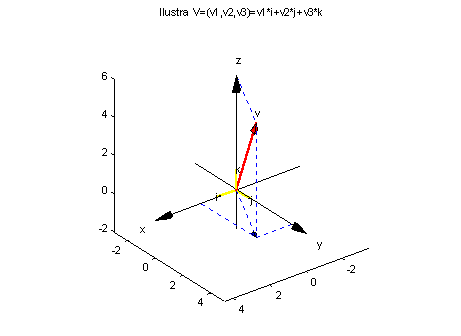
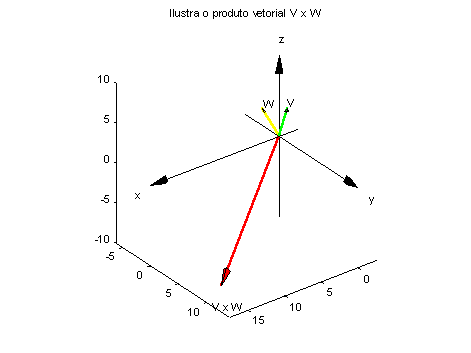
EDU» ilvxw(v,w)
% produto vetorial de v por w
EDU» box % retira a caixa em volta da figura
EDU» grid off % retira a grade da figura
EDU»
ilproj(w,v) % projeção de V em W
EDU» box % retira a caixa em volta
da figura
EDU» grid off % retira a
grade da figura

A
função demog21 demonstra todas as funções
gráficas de vetores do pacote GAAL.