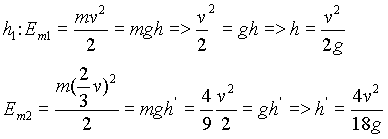
Trabalho de Cálculo 2 - UFMG / 1998.

Autores :Adriano Alonso Veloso : adrianov@dcc.ufmg.br

Alex Borges Vieira : borges@dcc.ufmg.br

Romeo de Assis Gresta : romeo@dcc.ufmg.br

Professora : Sylvie : syok@mat.ufmg.br

Qualquer dúvida ou segestão favor entrar em contato com um dos endereços acima.


Introdução :

O trabalho consistia em analisar o movimento descrito por uma bolinha ao ser liberada de certa altura h e que após cada choque perdia certa quantidade de energia (sua velocidade era reduzida a 2/3). Seguindo princípios básicos de física e de séries numéricas fomos capazes de analisar e resolver os problemas propostos.

  1. Altura atingida apos cada choque:

 

Examinando os primeiros casos percebemos o seguinte :

 

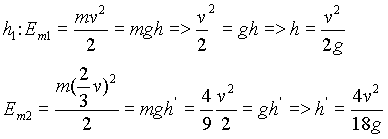
Ou seja, após cada choque a bola sobe a uma altura menor que a atingida anteriormente. Vemos também que há uma razão entre essas alturas. Observando os casos anteriores Concluimos entao que a razao entre cada altura é ,

logo: 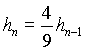, onde e a altura atingida apos o choque e

e a altura que a bola cai antes do choque.

Para o caso geral temos :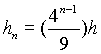

Para resolver esse problema nós usamos o princípio de 'conservação da energia do sistema'.

 

  1. Tempo decorrido entre dois choques consecutivos:

- Analisando os Primeiros casos temos verficamos o seguinte:

Obs: Tempo de subida = Tempo de descida

 

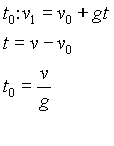(só para descer)

Após cada choque a velocidade se reduz a e o tempo e multiplicado por 2 devido a subida e a descida, então:

 

 

 

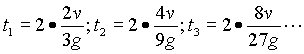
Logo, pela analise dos casos verificamos que o tempo entre os choques também segue uma razão. Concluímos a partir daí que o tempo entre choques é Tn =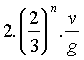

Nós usamos nesse problema equações de queda livre (movimento acelerado).

 
  1. Mostrar que a bola para após um tempo finito
    2.

 

 

Þ Para isso podemos mostrar que o tempo entre 2 choques tende a zero para choques distantes (ou seja , os últimos choques). Para isso analisamos o tempo entre o n-ésimo e o n+1-ésimo choque (n muito grande).

Temos que o tempo entre 2 choques é : é Tn =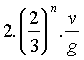

Para n muito grande temos que o tempo é dado pelo ‘Limite’ a seguir:

 

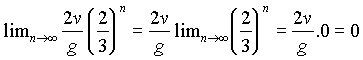
Esse resultado já era esperado pois senão a bola ficaria saltando para sempre, o que observamos na prática ser impossível !.

 

 

  1. Distância total percorrida pela bola

    2.  

    A bola percorre a altura inicial mais duas vezes cada altura a partir daí. Basta então somarmos a primeira altura, mais duas vezes as demais. Podemos obter as demias a partir do somatório das alturas (de 2 a infinito). Temos então:

     

     

     

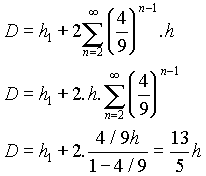
  2. O que ocorreria com esses valores se fosse na Lua.

 

Na lua, como a gravidade é menor , os valores das alturas, tempos decorridos entre dois choques e distância total percorrida iriam aumentar, mas ainda assim a bola iria parar. Podemos exemplificar isso com a altura entre dois choques. Suponhamos que o valor da gravidade da Lua e a metade da gravidade da terra .

 

Examinando os primeiros casos:

 

H1 : Em1 = mv2/2 = mgh/2 è v2 = gh è h = v2/g

H2 : Em1 = m(2/3v2)/2 = mgh/2 è 4v2/9 = gh è h = 4v2/9g

 

Podemos observar claramente que esses valores são maiores que os da terra !! Como já dito antes o mesmo ocorre para os demais valores !!