1^o Projeto de Cálculo 2

Arthur Toledo

Daniel Vasconcelos

Paulo Vialleti

 

Professora: Sylvie Oliffson Kamphorst

1.2 Curva de Koch

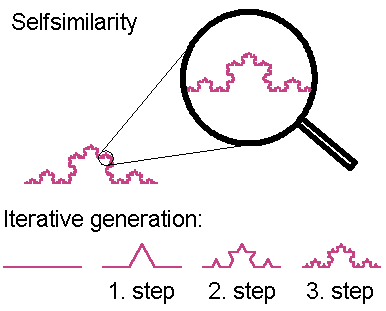
1. A Curva de Koch é uma curva plana, definida recursivamente. Sua lei de formação é descrita da seguinte maneira: Considere um segmento de tamanho 1. Divida esse segmento em 3 partes iguais, remova o segmento do meio. Em seu lugar, coloque 2 segmentos de mesmo tamanho do segmento removido de modo a formar a parte de cima de um triângulo. Obtivemos 4 segmentos de mesmo tamanho. Agora, repetimos o processo, recursivamente, para cada um dos 4 segmentos. A soma dos comprimentos será cada vez maior.

2. Dividiremos recursivamente por , um determinado comprimento e somamos o valor dessa divisão ao valor anterior do comprimento:

S_o = 1

S₁ = 1 + =

S₂ = + =

S₃ = + =

S_n = S_n-1 + =

lim S_n = +

A soma do tamanho do comprimento quando as iterações (repetição do processo) tendem a um número infinitamente grande, a medida do comprimento também tende para um número infinito. Isso ocorre devido a soma de uma quantidade de segmentos cada vez maior, pois soma-se ao comprimento anterior sua terça parte. Com isso, o tamanho tende ao infinito.