Um planeta movimenta-se em torno do sol num caminho polar dado por:

1: Verifique que o caminho é uma elipse:

2: Calcule o periélio ( a menor dist6ancia do sol ao planeta ):

Seja r o raio que une o centro do sistema polar ao ponto móvel P. Sabemos que a relação entre o raio e o ângulo ente o eixo polar o segmento que une o centro ao ponto é:

Vejamos o que acontece quando o angulo varia de 0 até 360 graus.

Marcando-se os pontos, obtêm-se o seguinte gráfico:

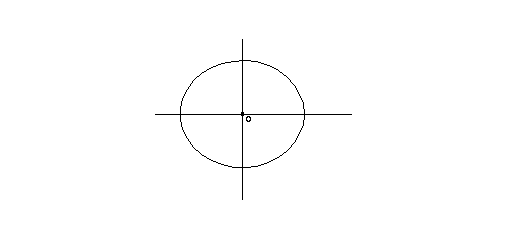É claro que o simples desenho não prova que a figura em questão é uma elipse.

Tal demonstração é feita mediante a substituição do sistema de coordenadas, ou seja, do sistema polar para o sistema cartesiano.

Para a substituição, usamos das seguintes relações entre r, x e y:

Assim, temos os seguintes cálculos:

Tendo feita a mudança no sistema de coordenadas, obtém-se este novo desenho:

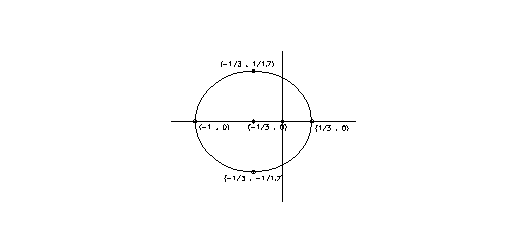As coordenadas focais podem ser obtidas através da seguinte relação entre as medidas dos eixos da elipse:

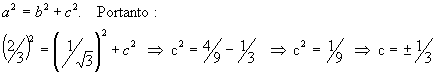
Sendo 2c a distância que une os dois focos da elipse, temos que as coordenadas cartesianas dos focos são: F(-2/3,0) e F1(0,0). Veja o gráfico abaixo: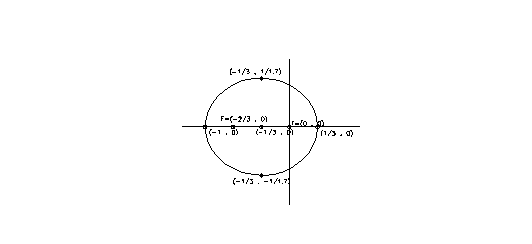

Como a elipse corresponde à orbita de um planeta em torno do sol, a distância mais próxima entre os dois corpos ocorre no eixo horizontal. Seja D tal distância:

D = a –c D = 2/3 – 1/3 D= 1/3.

Desse modo, podemos concluir que o periélio solar mede 1/3 da unidade de medida em questão.