Cálculo 2
Alex Borges - borges@dcc.ufmg.br
Adriano Alonso - adrianov@dcc.ufmg.br
Romeo de Assis - romeo@dcc.ufmg.br
-= fonte : Simmons, Cálculo com Geometria Analítica Vol. 2 =-
Representação paramétrica da Circunferência, Elipse, Parábola.
Considere uma circunferência de raio "a", centro na origem e que passa pelo ponto P(x,y).![]()
Sendo assim,
Quando o ângulo varia de 0 a 2p , o ponto P(x,y) parte de (a,0) e completa uma volta no sentido anti-horário.
![]()
Para obter a equação cartesiana dessa circunferência, é só observar que :
![]()
Agora considere elipse. Sua equação genérica é:
![]()
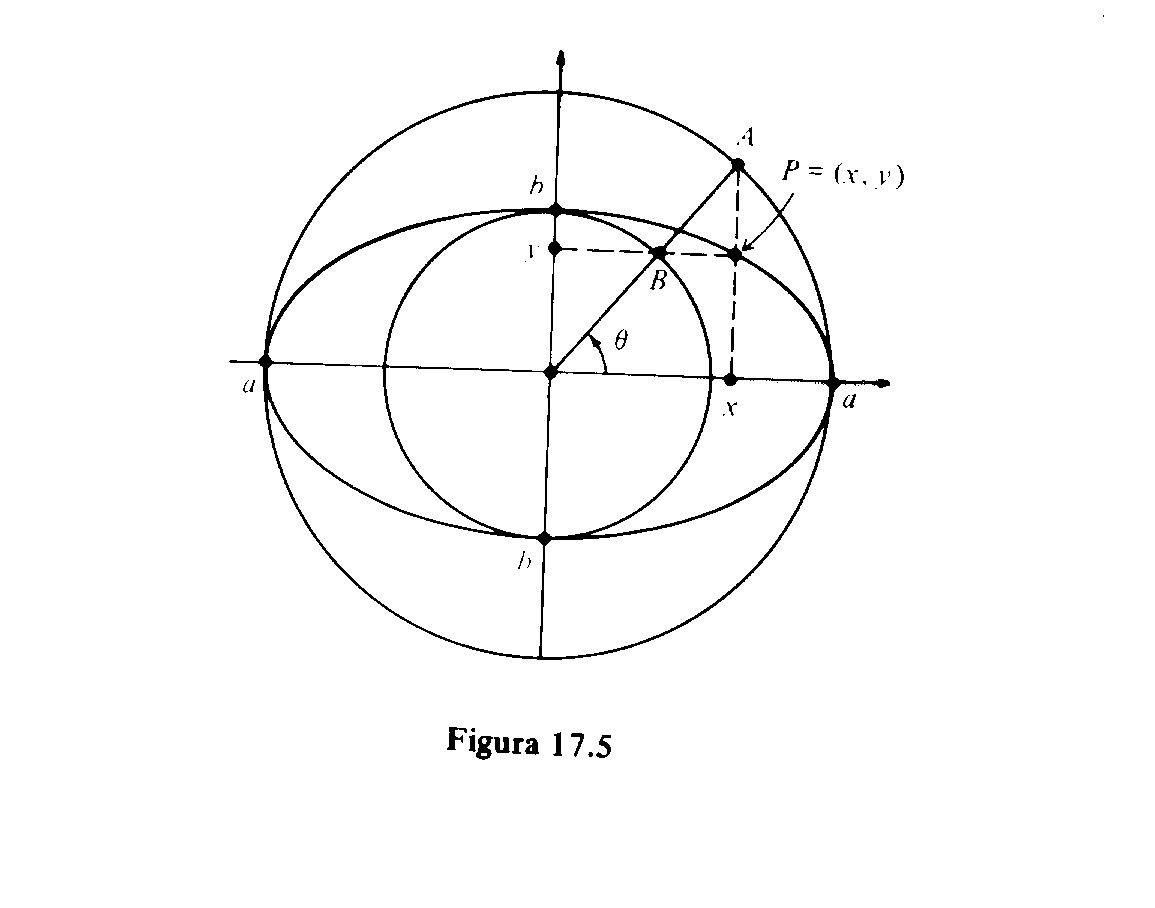
Esta elipse pode ser parametrizada fazendo-se as seguintes considerações:
![]()
Quando o ângulo varia de 0 a 2p , o ponto P(x,y) parte de (a,0) e completa uma volta no sentido anti-horário.
O ângulo q não é o ângulo central da elipse. Ele é o ângulo central subentendido pelos arcos determinados pelo eixo polar e pelos pontos A e B sobre as duas circunferências, uma circunscrita e a outra inscrita na elipse.
O ponto P é a interseção da reta vertical por A com a reta horizontal por B.
Agora vamos falar sobre a parábola. Sua equação genérica é:
![]()
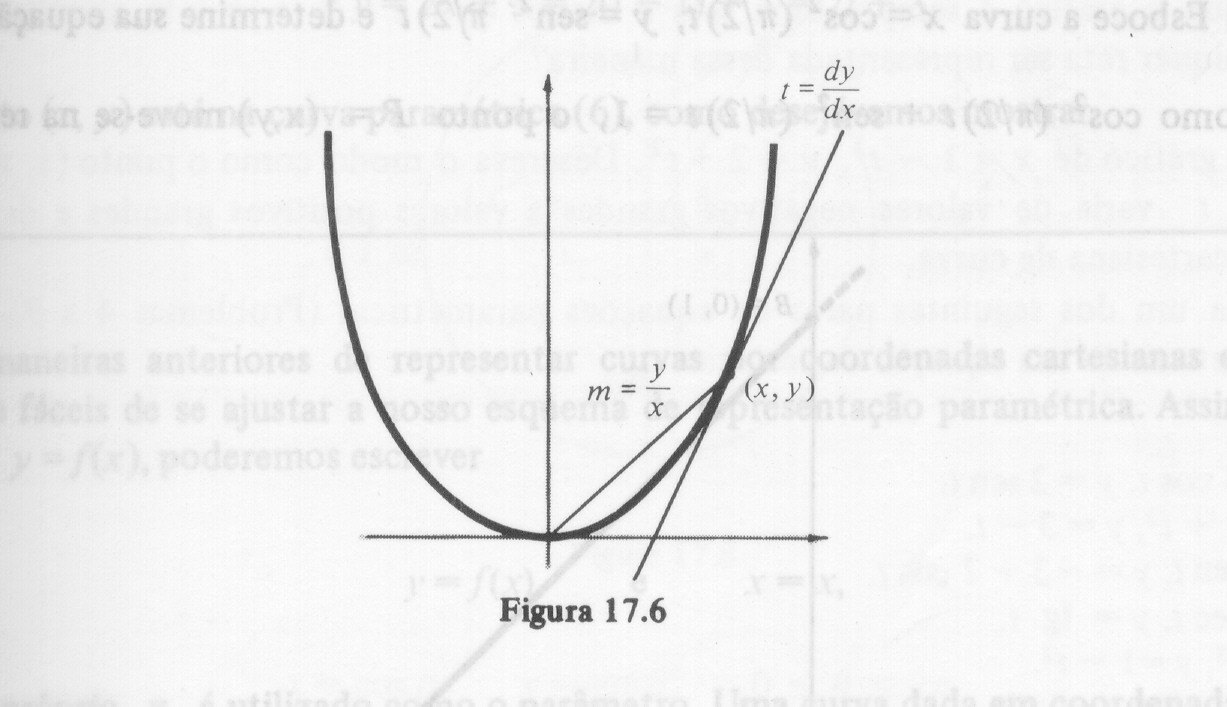
 A parábola pode ser parametrizada de muitas maneiras. Vamos utilizar o coeficiente angular da tangente em (x,y) com parâmetro,
A parábola pode ser parametrizada de muitas maneiras. Vamos utilizar o coeficiente angular da tangente em (x,y) com parâmetro,
Em cada caso a parábola completa é traçada quando o parâmetro cresce de -¥ a ¥ .
2.6 Telescópio Cassegrain
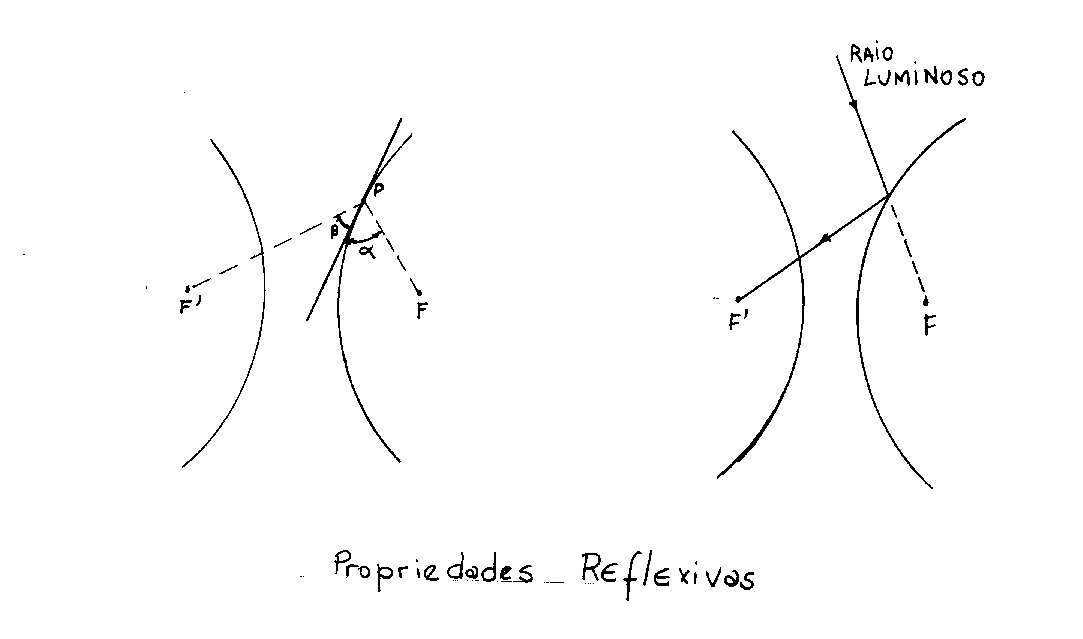
As hipérboles possuem uma propriedade reflexiva: a reta tangente em qualquer ponto P da hipérbole é a bissetriz do ângulo formado pelos segmentos de reta PF e PF’, onde F e F’ são os focos da hipérbole; PF e PF’ são chamados raios focais. Isso implica que a = b (veja figura a seguir). Assim, se a hipérbole for girada ao redor de seu eixo principal a fim de se formar uma superfície de revolução e se os lados convexos de cada parte tornarem-se superfícies refletoras, os raios de luz que se aproximam de um lado convexo por uma trajetória que passa pelo foco serão refletidos na direção do outro foco.
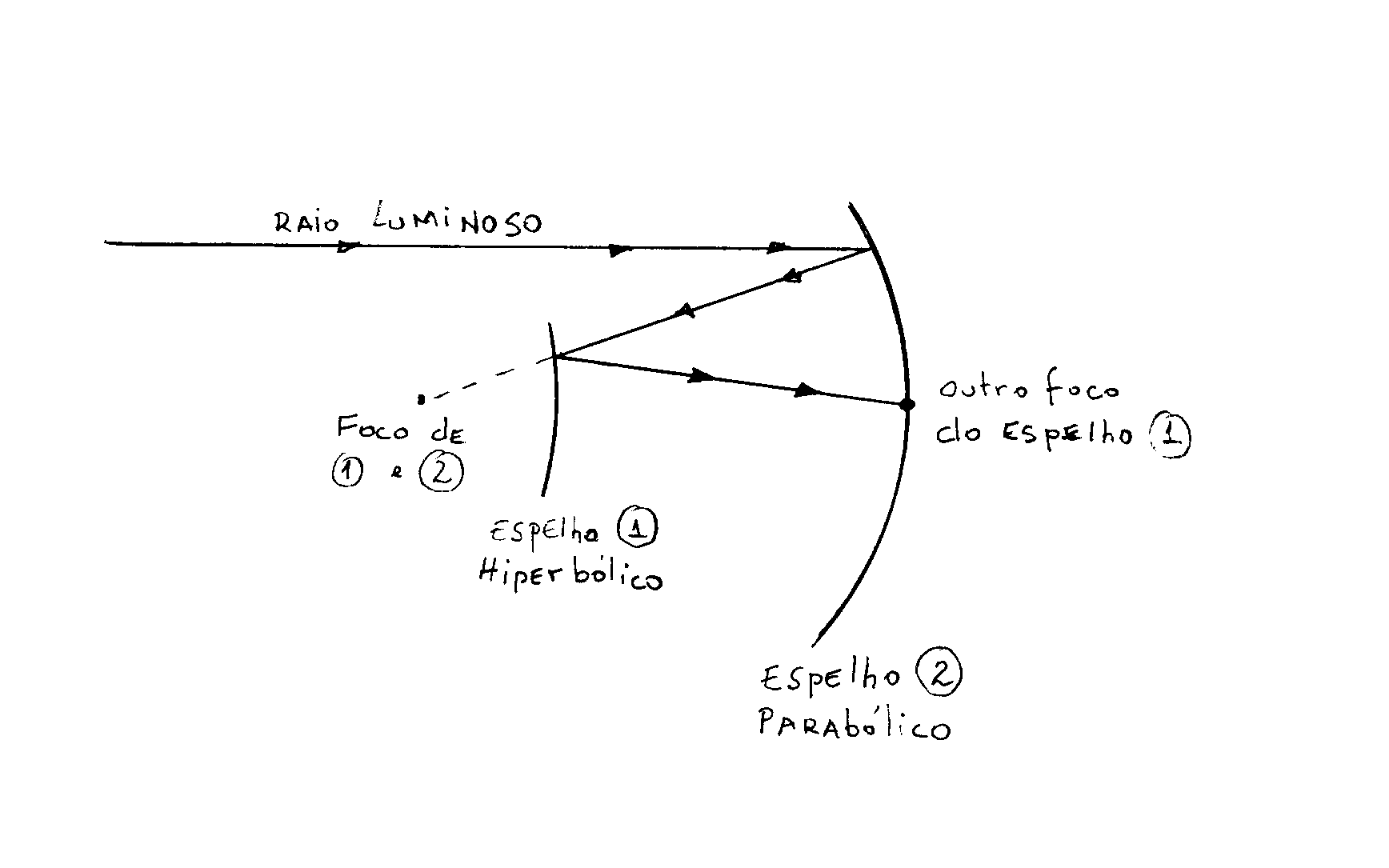
Tal propriedade reflexiva é o princípio essencial no projeto de telescópios refletores do tipo Cassegrain (veja figura a seguir). Como mostra o desenho, o foco do espelho hiperbólico coincide com o foco do espelho parabólico e o outro foco do espelho hiperbólico está sobre o vértice do parabólico, onde geralmente coloca-se um ocular ou uma câmera. Raios débeis de luz estelar são refletidos primeiramente pelo espelho parabólico em direção ao seu foco, mas são refletidos pelo espelho hiperbólico em direção ao vértice do parabólico, onde pode ser visualizado pelo ocular ou pela câmera.
Pequena Observação sobre Cometas :
Existem dois tipos de cometas. O primeiro tipo consiste em cometas que pertencem ao sistemas solar, viajam eternamente ao redor do Sol e descrevem assim órbitas elípticas com o Sol ocupando um dos vértices. O segundo tipo possui cometas que entram no sistema solar em altas velocidades, voltejam ao redor do Sol e depois saem do sistema solar, voltando ao espaço, descrevendo assim órbitas hiperbólicas com o Sol. O fator determinante dessas trajetórias é a energia total (E) do cometa, que é constituída de energia cinética(devida a seu movimento) e de energia potencial(devida à atração gravitacional do Sol). Verifica-se que se E < 0 , a órbita é uma elipse, e se E > 0 a órbita é uma hipérbole. (O caso E = 0 corresponde a uma órbita parabólica, mas é bastante improvável.)