Projeto De Cálculo
A propriedade reflexiva da Parábola
Marco Aurélio
Izabella Lyon
Alexandre Alves
![]()

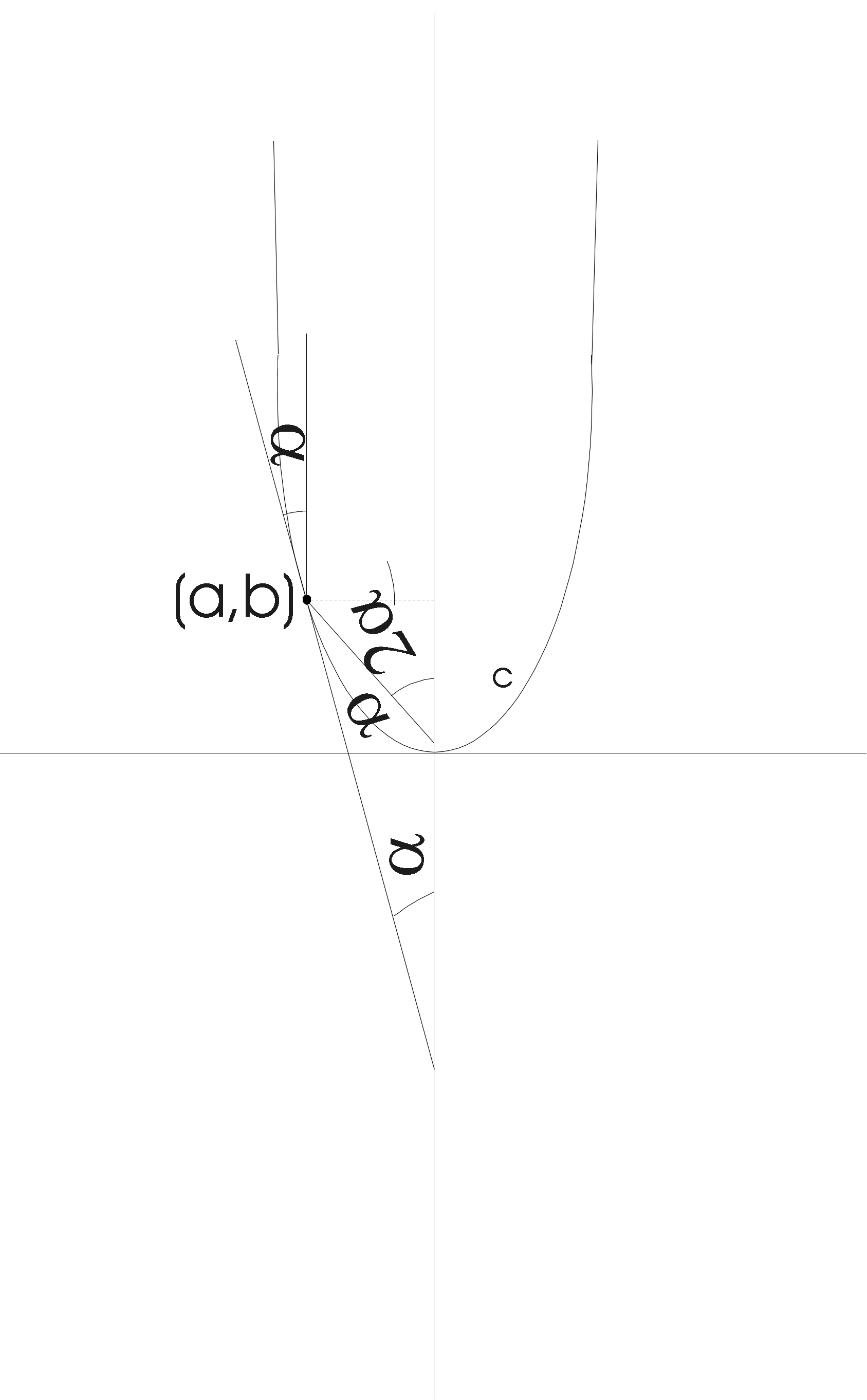
Considerando p como a distância do vértice ao foco da parábola e utilizando a fórmula padrão y2 = 4px, temos y = 2
Ö px.Vamos imaginar que a parábola possui sus superfície interna espelhada e que um feixe de luz incida paralelamente ao eixo vertical da parábola, sobre essa superfície. Este ponto de incidência terá as coordenadas (a,b) e possui a propriedade de que o ângulo de incidência é igual ao ângulo de reflexão em relação a reta normal por este ponto. O raio refletido corta o eixo vertical num ponto que dista c unidades do vértice.
Calculando-se a inclinação da reta tangente à parábola chagamos às seguintes relações:
dy
= 2Ö p = Ö ( p/x) ; tg a = Ö (p/a)dx 2
Ö x
Mas pelo gráfico sabemos que:
tg
a = b ; tg 2a = 2 tg a .a - c 1 - tg2
ab = 2
Ö (p/a) = 2 Ö p a .a - c 1- (p/a) a - p
b = b .
a - c a - p
Logo, concluímos que c = p, ou seja, todo raio que incide paralelamente ao eixo vertical reflete passando pelo foco.
Algumas aplicações práticas desta propriedades reflexiva.