Carlos Eduardo Carvalho de Andrade
Projeto 02
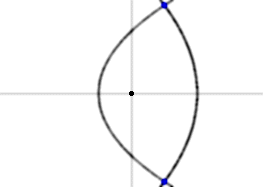
A parábola y2 = 4p (x + p) tem seu foco na origem e eixo ao longo do eixo-x. Atribuindo-se diferentes valores a p, obtém-se uma família de parábolas confocais, conforme a figura na página 125 do livro. Famílias deste tipo ocorrem em estudos de eletricidade e magnetismo.
(a) Mostre que há exatamente duas parábolas da família que passam por um ponto dado P (x1, y1) se y1 ≠ 0.
(b) Mostre que as duas parábolas em (a) são mutuamente ortogonais - isto é, as tangentes em P (x1, y1) são perpendiculares.

(a)
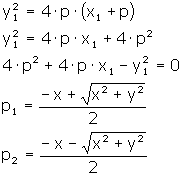
Para cada ponto (x1, y1), foram encontrados p1 e p2 distintos, portanto, há duas parábolas da família que passam pelo ponto (x1, y1). O foco das parábolas é (0, 0) e os vértices são (0, -pn).
(b)
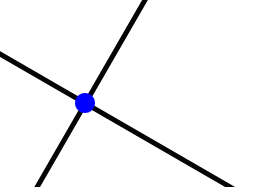
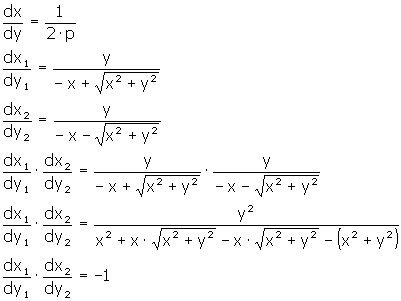
O produto dos coeficientes angulares das duas parábolas é igual a -1. Portanto, as duas parábolas são mutuamente ortogonais.