Considere a área delimitada pela parábola de equação y = ax e uma reta paralela à diretriz (reta r) desta parábola . A figura formada possui base igual a b e distância do vértice à reta r igual a h.

Se traçarmos o eixo coordenado xy de tal forma que, a origem desse coincida com o vértice da parábola, teremos a seguinte figura:

A base da figura está sobre a reta r (y = h) e a parábola é simétrica ao eixo y, dessa forma, encontramos o ponto P (b/2,h) onde as duas retas se interceptam no primeiro quadrante.

A área delimitada pelas retas pode ser calculada utilizando o cálculo integral:

Iremos calcular a área assinalada em amarelo na figura, o resultado, multiplicado por dois, dará a área total procurada.

b/2

0

b/2 b/2

0 0

Calculando a em função de b e h:

a = h/ (b/2) ²

a = 4h/b²

Substituindo a na equação 1 :

A = h(b/2) - 1/3 (4h/b² ) ( b³/8) - 0

A = (hb)/2 - (hb)/6

A = (3hb - hb)/6

A = hb/3

A área total procurada é duas vezes a área A :

A = 2hb/3

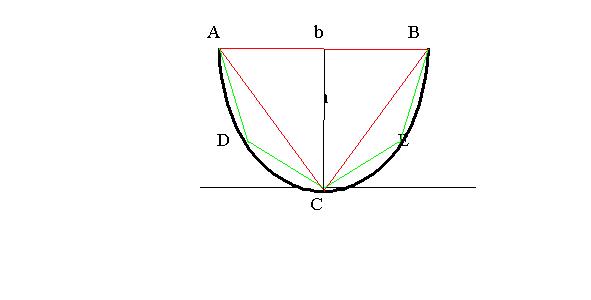
O processo, utilizado por Arquimedes , para calcular a área de um seguimento parabólico, consiste em tomarmos o triângulo ABC, onde C corresponde ao ponto em que a tangente e paralela à reta AB. Para o seguimento descrito anteriormente, teremos AB correspondente à base da figura e C ao vértice (0,0).

Em seguida, escolhemos D e E, pontos onde as tangentes são paralelas a AC e a BC, formando assim, os triângulos ADC e BCE. Para calcularmos a área devemos repetir esse procedimento até exaurirmos o seguimento parabólico.

A área do triângulo ABC e quatro vezes a soma das áreas dos triângulos

ACD e BCE: ACD + BCE = ¼ ABC.

A soma das áreas dos próximos triângulos tomadas duas a duas será:

¼ ACD + ¼ BCE

¼ (ACD + BCE)

¼ ² ABC

Repetindo esse procedimento indefinidamente, teremos:

Área Total = ABC + ¼ ABC + ¼² ABC + ...

Área Total = ABC ( 1 + ¼ +1/16 +...)

A Soma geométrico (1 + ¼ + 1/16 + ...) = 1/(1-r) ,onde r = ¼

Soma = 4/3

Área Total = 4/3 ABC

A área do triângulo ABC = (b h)/2

Área Total = 2bh/3