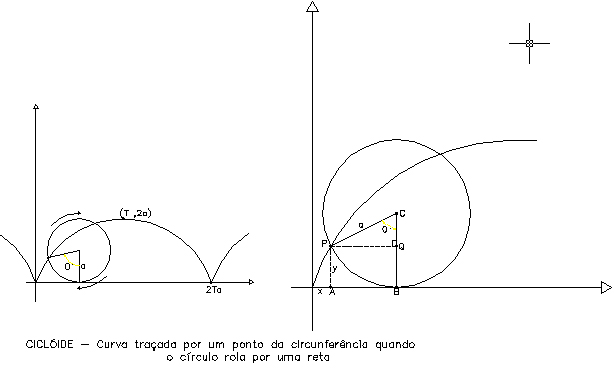
A ciclóide é a curva traçada por um ponto fixo P da circunferência de um círculo quando o este rola, sem deslizar, por uma reta.

O único modo conveniente de representar uma ciclóide é por meio de equações paramétricas. Supomos que o círculo rolante tem raio a e que ele rola sobre o eixo x, começando de uma posição em que o centro do círculo está no semi-eixo positivo dos y. A curva é o lugar geométrico do ponto P da circunferência, localizado na origem O quando o centro C está no eixo y. O ângulo 0 da figura é o ângulo varrido pelo raio CP quando o círculo rola para uma nova posição. Se x e y são as coordenadas de P, então o giro do círculo implica que OB = arco BP = a 0, logo, x = OB – AB = OB – PQ = a 0 – a sen 0 = a (0 – sen 0). Também y = BC – QC = a – a cos 0 = a (1 – cos 0). Portanto a ciclóide tem a representacao parametrica:

x = a (0 - sen 0)

y = a (1 - cos 0)

Sendo a < 0, o gráfico de x = a(t – sen 0), y = a (1 – cos 0) é a ciclóide invertida obtida quando o círculo rola abaixo do eixo x. Um segmento de tal curva é denominado braquistócrona, tendo a seguinte propriedade: Na descida de um ponto A a um ponto B, uma pequena bola que deslize livremente numa rampa, tendo como única forca atuante a gravidade, chegará mais rapidamente ao ponto B se a rampa em questão estiver de acordo com as equacoes da braquistocrona, que significa descida mais rapida, daí o nome dado à curva.

Outra propriedade curiosa de tal curva é que, de qualquer ponto da rampa que esteja o ponto A, o tempo para a esfera chegar a B é sempre o mesmo.

Fernando Linhares

Hugo Pinto

Jose Luiz Bastos Jr.