EQUAÇÃO PARAMÉTRICA DO PLANO

Parametrização de um Plano

Um plano no espaço é um objeto bidimensional, logo ele precisa de uma equação em dois parâmetros para descrevê-lo. Em outras palavras, precisamos de duas coordenadas para determinar cada ponto do plano (pense no plano xy , por exemplo). Contraste esta situação com a de uma reta no espaço: a reta, sendo um objeto unidimensional, precisa de apenas um parâmetro t para ser descrita.

Outra maneira de ver que precisamos de dois parâmetros para descrever completamente um plano, é considerar o seguinte. Como já vimos anteriormente, a equação geral de um plano no espaço que passa pelo ponto e é perpendicular ao vetor é

ax + by + cz = d

onde . Nesta equação, duas das variáveis são livres, isto é, podem assumir valores arbitrários independentes; a terceira variável fica determinada em função dos valores destas duas. Por exemplo, se a não é zero, podemos escolher y e z como variáveis livres e atribuir a elas valores arbitrários independentemente, digamos, e . Daí a variável x fica determinada: necessariamente, 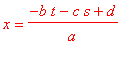. Portanto, um ponto pertence ao plano se e somente se

para algum t e para algum s . O que fizemos também pode ser entendido do ponto de vista da resolução de sistemas lineares. De fato, a equação geral do plano nada mais é que um sistema de uma equação em 3 incógnitas, que pode ser resolvido escalonando a matriz:

Este sistema possui apenas um pivô, situado na primeira linha, logo duas variáveis devem ser livres. As duas variáveis livres são os dois parâmetros da equação paramétrica do plano.

Exemplo

Dado o plano cuja equação geral é x + 2 y - z + 5 = 0 , determine a equação paramétrica deste plano.

Solução: Primeiro isolamos uma das variáveis em função das outras duas. Para facilitar os cálculos isolamos z :

z = x + 2 y + 5

Portanto, isso significa que escolhemos x e y como variáveis livres. Atribuindo a elas valores arbitrários, digamos x = t e y = s , obtemos a equação paramétrica do plano :

Gráficos

Os gráficos animados mostram o plano sendo gerado quando fazemos os parâmetros t e s percorrerem todos os valores reais. No primeiro gráfico, para cada valor fixo do parâmetro t , ao variarmos o parâmetro s obteremos uma reta; logo, como existem infinitos valores de t , existem infinitas tais retas. Retas deste tipo estão representadas no gráfico pelo movimento da reta azul . Se, por outro lado, fixarmos o parâmetro s e variarmos o parametro t teremos retas do tipo da reta vermelha representada no segundo gráfico, e como existem infinitos valores de s percorrendo o conjunto dos números reais, isso é representado pelo movimento da reta vermelha no gráfico. Tanto a reta azul como a reta vermelha varrem completamente todo o plano.